§5. Геометрическое определение вероятности от репетитора по теории вероятностей Александра Быстрова.

Если результат испытания определяется случайным положением точки в некоторой области, причем любые положения точек в этой облас¬ ти равновозможны, то при этом используется геометрическое определение вероятности.

А именно, вероятность события равна

\(P=\frac{S_{0}}{S}\)

где \(S\) - размер / т.е. длина, площадь, объем / всей области,

\(S_{0}\) - размер той части области, попадание в которую благоприятствует дан¬ ному событию.

Пример1 от репетитора по теории вероятности Александра Быстрова.

В квадрат вписан круг. Какова вероятность, что точка

наудачу брошенная в квадрат, окажется внутри круга. Решение от репетитора по теории вероятности Александра Быстрова.

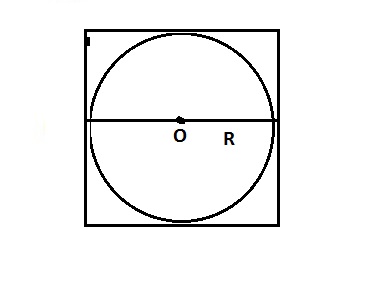
Площадь квадрата \(S=4R^2\)

Площадь круга \(S_{0}=π R^2\)

Вероятность равна \(P=\frac{π R^2}{4R^2}=\frac{π }{4}\)

Пример 2. От репетитора по теории вероятности Александра Быстрова.

На отрезок ОА длины \(L_{0}\) числовой оси брошены наугад две точки В и С , причем точка С расположена правее точки В. Найти вероятность того, что длина отрезка ВС меньше длины отрезка ОВ.

                            y

| _______________________________|

             x

|________________|                                         \(L_{0}\)

-------[-------------------------х----------------------х---------------х]--------------------------------

       0                        B                      C                A

                                                                          \(L_{0}\)

Решение от репетитора по теории вероятности Александра Быстрова.

Обозначим х и у координаты точек В и С соответственно. Координаты точек В и С должны удовлетворять неравенствам:

\(0=< x =< L0 ; 0=< y =< L0 ; y > x\)

Выразим эти условия на плоскости

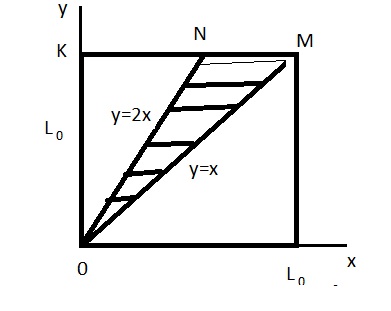
Указанным неравенствам удовлетворяют координаты любой точки треугольника ОКМ. Длина отрезка ВС равная \((у-х)\) должна быть меньше длины отрезка ОВ /х/, то есть

\(y - x < x\) или \(y\)

Координаты точек благоприятствующих выполнению условия задачи является треугольник ONM. Искомая вероятность равна:

\(P=\frac{(0,5 (L_{0})^2 - 0,5L_{0} 0,5L_{0})}{ 0,5 (L_{0})^2}=\frac{0,25 (L_{0})^2}{0,5 (L_{0})^2}=0,5\)

 Ответ: \(0,5\)