Репетитор по математике 11 класс

Отзывы учеников и родителей

Успешный репетитор по математике - 11 класс -  Александр Анатольевич Быстров, кандидат  физ.-мат. наук, докторант, имеющий педагогический стаж более 17 лет (Московский энергетический институт, технический университет), подготовит к экзамену. Опыт репетитора по математике - 11 класс-  более 20 лет. Имеет лучшие показатели по качеству подготовки. Более 120 учащихся поступили  в ВУЗы,  университеты и институты  Москвы: ВШЭ, МЭИ, МВТУ им. Баумана, МАИ, МАДИ, Финансовый Университет при Правительстве Москвы, МИРЭА, НАХ им.Плеханова, МГУ, и многие другие. Занятия провожу индивидуально в офисе на м. Китай-город. Стоимость занятий оговаривается индивидуально и зависит от сложности.  
 
Репетитор по математике - 11 класс-  обучает решению примеров по тригонометрии, иррациональным уравнениям, уравнениям и неравенствам с логарифмами и показательными функциями, задачам экономическим, по геометрии и стереометрии. В процессе индивидуальных занятий с учащимся выпускниками  выясняются с помощью периодического тестирования  слабые стороны, те части математики, которые  плохо были усвоены. Проводится работа по объяснению формул, теорем и выражений, необходимых для отличной сдачи экзамена.  На простых примерах показывается, как быстро и правильно получить ответ. Чтобы получить высокий балл репетитор  по математике - 11 класс - особую роль уделяет точному решению  тригонометрических уравнений. Не малую сложность, как показывает большой опыт, вызывают неравенства с логарифмами. Если ученик усвоил указанный материал с ним разбираем  примеры с параметрами. Для успешной сдачи экзамена необходимы регулярные занятия 1-2 раза в неделю. Чтобы убедиться в успешности  работы преподавателя изучите отзывы. О нем говорят, как о прекрасном учителе и человеке.  

Большой педагогический опыт занятий с учащимися выпускного класса позволяет мне, репетитору по математике для 11 класса после первого занятия определить слабые стороны ученика. Даже хорошисты и отличники в школе при решении задач 
демонстрационный вариант ЕГЭ 2017 по математике - профильный уровень делают ошибки. Некоторым не даются задачи по геометрии и стереометрии. Другие буксуют на текстовых задачах (№11) и производных. Школьные хорошисты часто делают ошибки в тригонометрических уравнениях (№13) и редко умеют правильно решить неравенства особенно, если есть логарифмы (№15). Самый "голодный минимум" для молодого человека сдать достойно экзамен:  получить плюсы или правильные ответы в по всем задачам первой части (№1-№12), решить №13 и главное написать  правильное решение, и если есть знания - №15. Тогда балл будет составлять 70-72. С таким баллом можно поступить на бюджет во многие экономические и технические университеты. Но, конечно, для умного школьника -это не предел. Репетитор по математике для учеников 11 класса говорит:"Если он осилит №14, при правильных от №1 -№15, то получит 75 баллов". Для набора выше 75, необходимо решить геометрическую задачу №16-78, экономическую(№17)-85-87  и задачу на параметры №18- 90-95.   Как правило, тот кто задумал поступить на бюджет в приличный университет и на приличный факультет должен набрать 70 - 80 баллов.

Пересдать экзамен по математике профильный уровень и набрать вполне необходимое количество баллов – это далеко полностью не решает всех проблем! В большом ряде ведущих ВУЗов и университетов Москвы,например, некоторых технических университетах, поступающим нужно сдавать ещё и специальный, профильный экзамен по одному из предметов. Благополучно подготовиться к этому в достаточной мере непростому по требованиям экзамену поможет Вам опытный репетитор по математике в 11 классе Быстров Александр Анатольевич. При этом, бесспорно, профильный экзамен абсолютно соответствуют программам средней школы. Наиболее горестное - это, поступив в ВУЗ Москвы ,например, Московский энергетический институт МЭИ или Московский физико-технический институт МФТИ необходимо остаться в нём, не быть отчисленным за неуспеваемость на первом или втором курсах.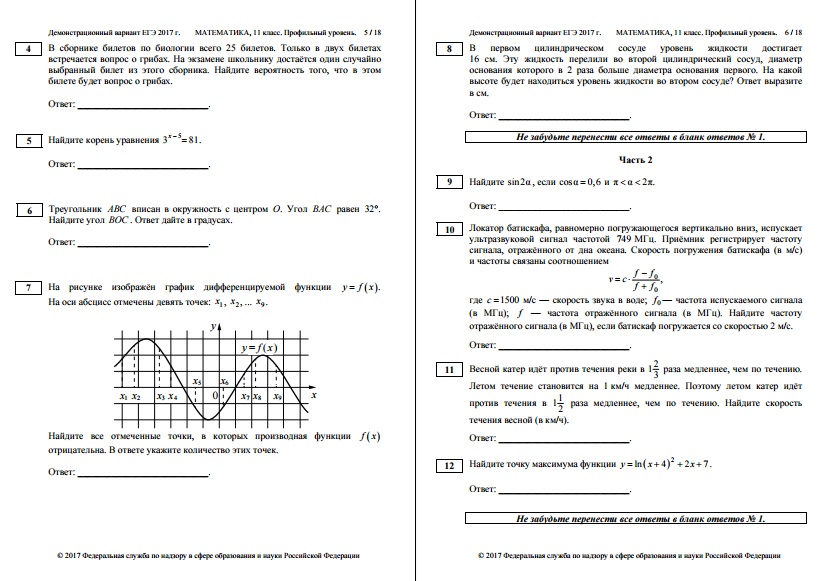

Практика представляет, что эта проблема мало заботит поступающих в ВУЗы и их родителей в накаленный и в достаточной степени суровый период подготовки к сдаче экзамена. Эту проблему несомненно помогут решить регулярные занятия с репетитором по математике для 11 класса Быстровым Александром Анатольевичем . Мы, преподаватели ВУЗов, ведаем, что из года в год имеет место довольно неутешительная статистика отчислений студентов младших курсов за академическое отставание. Это связано с тем, что зачислившись в ВУЗ, свежеиспечённые студенты – молодые, нормальные, а, выходит, безмерно рассудительные люди - поступают в кардинально новейшие для них условия обучения и преподавания.

13. а) Решите уравнение   \(cos2x= 1 - cos( \frac{π}{2} - x)\) .

б) Найдите все корни этого уравнения, принадлежащие промежутку

\([\frac{-5π}{2} ; -π)\)

Договориться на первое занятие

Решение.а) Уравнение после преобразования запишем в виде:

\(1 - 2sin^{2}x =1 - sinx\);
\(2sin^2{x} - sinx  =0\) ;
\(sin x (2sinx- 1) = 0\) ,

следует
\(sinx=0 \)  и \(2sinx=1\) .

Далее из \(sinx=0\)
получаем:
\(x = πn\) , где \(n∈Z\).

Получаем из
\(sinx=\frac{1}{2}\) , что  \(x=\frac{π}{6}+2πn\) и \(x=\frac{5π}{6}+2πn\) , где \(k∈Z\).

б) Рассмотрим  числовую окружность: 

корни уравнения, принадлежащие промежутку

\([\frac{-5π}{2} ; -π)\) .

Получаем числа: \(-2π\) ; \(\frac{-11π}{6}\) ; \(\frac{7π}{6}\) .

Ответ: а) \(x=\frac{π}{6}+2πn\) и \(x=\frac{5π}{6}+2πn\)

б) \(-2π\) ; \(\frac{-11π}{6}\) ; \(\frac{7π}{6}\) .