Математический анализ. Решение задач на бесконечно малые. величины.

Задача 2.1

Для данных бесконечно малых при x→ x₀ величин записать эквивалентные

в виде A(x-x₀)^k :

1) ln(1+2x arctg((x)^5/3) ), x₀=0.

Решение:

Решение представляет репетитор по математическому анализу Быстров Александр Анатольевич.

Для решения данной задачи вспомним таблицу бесконечно малых величин при x→ 0 :

 таблица 1.1

1a	tgα(x)∼α(x)
2b	sinα(x)∼α(x)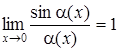
3c	(1- cosα(x))∼(α(x))2/2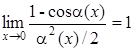
4d	exp(α(x))-1∼α(x)
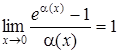5e	arctgα(x)∼α(x)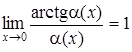
6g	arcsinα(x)∼α(x)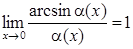
7i	ln(1+α(x)) ∼α(x)
8f	loga(1+α(x)) ∼α(x) /(lna)
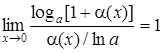9k	(1+α(x))1/n∼α(x)/n
10z	Aα(x)-1∼α(x)lnA

В данном примере применим формулу 

  ln(1+α(x)) ∼α(x) 

Тогда  ln(1+2x arctg((x)^5/3) ) ∼2x arctg((x)^5/3) ∼

далее  воспользуемся формулой arctg(α(x))∼α(x)  и тогда запишем

∼2x (x)^5/3 ∼2x¹ x^5/3=2x^1+ 5/3=2x ^8/3.

Ответ: ln(1+2x arctg((x)^5/3)) ∼2x ^8/3  при x→0.

Задача 2.2

Для данных бесконечно малых при x→ x₀ величин записать эквивалентные

в виде A(x-x₀)^k :

2) (1+x sinx - cos2x), x₀=0.

В этом примере применим формулы из таблицы1.1

sinα(x)∼α(x)   и  (1- cosα(x))∼(α(x))²/2   .

Тогда формула запишется в виде 

(1+x sinx - cos2x)=(x sinx)+(1- cos2x)∼x x+(2x)²/2=x²+4x²/2=x²+2x²=3x²

^{Ответ:  (1+x sinx - cos2x)∼3x2}   при x→0.

Записаться на занятия с преподавателем по высшей математике и математическому анализу Быстровым Александром Анатольевичем можно здесь,

позвонив по телефону +7-985-761-13-60. 

Занятия проводятся в центре Москвы около станции м Китай-город. 

Отзывы студентов университетов и учеников школ