Пример 3: Емкостной делитель напряжения.

Заряд \(Q\) на конденсаторе \(С\) связан с напряжением \(V\) через него

\(Q = C·V\) (3.1)

Рассмотрим два конденсатора, \(C1\) и \(C2\), последовательно через источник переменного напряжения,

\(V = V0\) греху (2n футов), как показано на рисунке 3.1.

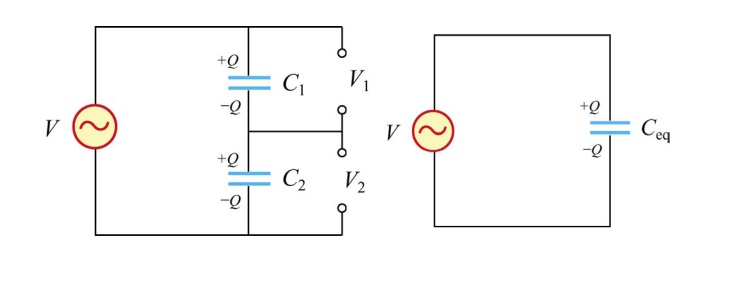
                                           Рисунок 3.1 Конденсаторный делитель  переменного напряжения.

Найдем напряжение на С2. Два конденсатора в цепи выглядеть как один конденсатор с эквивалентной емкостью равной

\(C_{eq}=\frac{C_{1}C_{2}}{C_{1}+C_{2}}\) ,

при этом ток,

\(I=\frac{dQ}{dt}\)

протекает через оба конденсаторов и производит тот же переменный заряд на них.

Затем ток

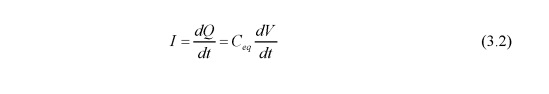
Таким образом, переменный заряд на два конденсатора становится через интеграцию

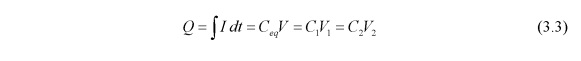
где V является напряжение на обоих конденсаторов в серии, а \(V_{1}\) и \(V_{2}\) напряжения на \(С_{1}\) и \(С_{2}\) соответственно.

Решение для \(V_{2}\) мы получаем, как

 \(V_{2}=\frac{Q}{C_{2}}=C_{eq}\frac{V}{C_{2}}=\frac{V}{C_{2}}\frac{C_{1}C_{2}}{C_{1}+C_{2}}=V(\frac{C_{1}}{C_{1}+C_{2}})\)                                        (3.4 )

Отношение V2 / V описывает делитель напряжения и задается

  \(\frac{V_{2}}{V}=\frac{C_{1}}{C_{1}+C_{2}}\)                  ( 3.5)

У нас есть то, что называется ёмкостной делитель напряжения для переменного напряжения,

который работает независимо от частоты, по крайней мере, в своей идеальной форме.

Пусть в делителе высокого напряжения \(C_{1}\) = 100 пФ и \(C_{2}\) = 1000 пФ. 

Тогда меньшее напряжения \(V_{2} = \frac{1}{11}V\) на конденсаторе, имеющего большую емкость \(C_{2}\), а

большее напряжения \(V_{1} = \frac{10}{11}V\) на конденсаторе \(C_{1}\). При сравнении с 

резистивным делителем, в котором  большее напряжение на большем сопротивлении, в емкостном делителе все наоборот.