§10.Биноминальное распределение вероятностей.Последовательность независимых испытаний.

Важные закономерности теории вероятностей, имеющие непосредственное применение в статистике, связаны с рассмотрением  независимых повторных испытаний.

Например бросается монета. Предыдущее испытание не влияет на последующее. Какова вероятность того , что при 10 бросаний монеты орел появится 3 раза.

Решение дается так называемой формулой Бернулли.

Вероятность появления события А в серии из n независимых испытаний ровно m  раз равна:

$P_{n}(m) =  C_{n}^m p^m  q^{n-m} =  \frac{ n!} {m! (n-m)!}  p^ m  q^{ n-m}$

где $p$ - вероятность появления события $А$ в каждом испытании, $q$- вероятность появления противоположного события.

По формуле Бернулли получаем, что при 10 бросаний монеты, вероятность появления орла 3 раза равна:

 $P_{n=10}(m=3) = C_{n=10}^{m=3}  p^{m=3}q^{n-m=7} =  C_{10}^{3} p^3 q^ 7=$

$= C _{10}^{3} (1/2)3(1/2)7 =\frac{17}{128}$

Пример 2. Вероятность попадания в цель при одном выстреле $р= 2/3$. Проводится 8 выстрелов. Найти вероятности возможных исходов / поражения мишени или промаха /.

Решение. Производится серия из $8$ независимых испытаний. По формуле Бернулли, вероятность  $m$ раз поразить мишень при $n =8$ выстрелах соответственно равны:

$m$

$C_{n}^{m}$

$P_{n} (m)$

0

$C_{10}^{0}$

$P_{n=8} (m=0)=(1/3)8≈0,0002≈0$

1.

$C_{8}^{1}$

$P_{n=8} (m=1)=8·(2/3)1·(1/3)7≈0,002≈0$

2

$C_{8}^{2}$

 $P_{n=8} (m=2)=28·(2/3)2·(1/3)6≈0,017$

3

$C_{8}^{3}$

 $P_{n=8} (m=3)=56·(2/3)3·(1/3)5≈0,068$

4

$C_{8}^{4}$

 $P_{n=8} (m=4)=70·(2/3)4·(1/3)4≈0,171$

5

$C_{8}^{5}$

$P_{n=8} (m=5)=56·(2/3)5·(1/3)3≈0,274$

6

$C_{8}^{6}$

 $P_{n=8} (m=6)=28·(2/3)6(·(1/3)2≈0,274$

7

$C_{8}^{7}$

 $P_{n=8} (m=7)=8·(2/3)7·(1/3)1≈0,156$

8

$C_{8}^{8}$

$P_{n=8} (m=8)=(2/3)8·(1/3)0≈0,038$

Полученные результаты можно представить графически /рис. 10.1/.В прямоугольной системе координат по горизонтальной оси откладываются числа $i$  /появление события А /, по вертикальной- значения вероятностей. Концы этих точек соединяются и получается многоугольник распределения.

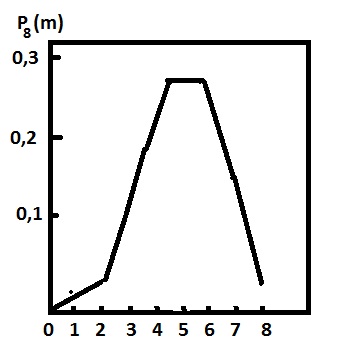
                                     рис. 10.1

Из рис. 10.1 видно , что при биноминальном распределении вероятностей

существует наивероятнейшее число появления события.

Наивероятнейшее число появления события A в серии n  испытаний находится из двойного неравенства:

$n·p - q    ≤    m_{0}  ≤     n·p + p$

Пример. Вероятность попадания стрелка  в цель равна 0,7.

Сделано 25 выстрелов. Определить наивероятнейшее число попаданий

в цель.

Решение. 

Здесь $n =  25 ,   p = 0,7 , q=0,3$ .

Следовательно, 

   $n·p - q    ≤    m0  ≤     n·p + p$

$25·0,7 - 0,3    ≤    m0  ≤     25·0,7 + 0,7$

$17,2    ≤    m0  ≤   18,2$

так как     $m$ - целое число, то  $m = 18$ .