§14. Числовые характеристики случайных величин. Математическое ожидание и дисперсия.

Закон распределения случайной величины полностью её определяет. Однако, часто важно знать основные параметры, характеризующие закон распределения в целом. Среди этих параметров наиболее важными являются математическое ожидание и дисперсия случайной величины.

1. Математическим ожиданием случайной величины называется сумма / или интеграл для непрерывной величины / произведений её значений на соответствующие вероятности.

а/. Математическое ожидание дискретной случайной величины равно:

 \begin{equation} M(x)=\sum\limits_{i=1}^n x_{i}p_{i}=x_{1}p_{1}+x_{2}p_{2}+...+x_{n}p_{n}  \end{equation}

б/. Математическое ожидание непрерывной случайной величины равно:

  \begin{equation} M(x)=\int\limits_{-∞}^{∞}xp(x)\,dx  \end{equation}

Замечание. Смысл математического ожидания состоит в том,что при большом числе испытаний среднее арифметическое наблюдаемых значений случайной величины близко к её математическому ожиданию.

2. Свойства математического ожидания

а/. Математическое ожидание постоянной величины равно:

 \(M(C)\)=\(C\), \(C\)=\(const\)

 б/. Выполняется равенство:

     \(M(Cx)=CM(x)\), при \(C=const\)

в/. Математическое ожидание суммы двух независимых случайных величин x и y равно:

\(M(x+y)=M(x)+M(y)\)

Определение. Случайные величины X и называются независимыми, если закон распределения каждой из них не меняется, когда становится известно , что другая приняла какое-либо значение.

г/ Математическое ожидание произведения двух независимых случайных величин \(x\) и \(y\) равно:

 \(M(xy)=M(x)·M(y)\)

Пример I. Проводится беспроигрышная лотерея на 200 выигрышей, из которых I выигрыш составляет IOO руб., 5'выигрышей по 20 руб., 10 выигрышей по 5 руб., и 184 выигрыша по 2 руб. Определить цену одного билета так, чтобы сумма выплаченных выигрышей равнялась сумме, вырученной за продажу билетов.

Решение. Составим таблицу распределения случайной величины /закон распределения/ \(x\)- сумма выигрыша:

Математическое ожидание данной случайной величины равно искомой цене билета:

  \begin{equation} M(x)=\sum\limits_{i=1}^n x_{i}p_{i}=2(184/200)+5(10/200)+20(5/200)+100(1/200)=3,09=3  \end{equation}

Пример 2. Дана плотность вероятности непрерывной случайной величины x :

                     0, x<0

р(x) =            0,5· sinx ,     0≤x≤π

                     0 ,  x>π

Найти математическое ожидание.

Решение. I. Сначала проверим, что для данной плотности вероятности выполняется необходимое условие:

\begin{equation} \int\limits_{-∞}^{∞}p(x)\,dx=1 ;  \end{equation} 

\begin{equation} \int\limits_{-∞}^{∞}p(x)\,dx=0,5\int\limits_{0}^{π}sin(x)\,dx=-0,5(cos(π)-cos(0))=1 ;  \end{equation} 

2. Математическое ожидание равно: 

\begin{equation} M(x)=\int\limits_{-∞}^{∞}xp(x)\,dx=0,5\int\limits_{0}^{π}xsin(x)\,dx=-0,5\int\limits_{0}^{π}x\,dcos(x)= \end{equation} 

\begin{equation} =-0,5xcos(x)+0,5\int\limits_{0}^{π}x\,dcos(x) =0,5(π+sin(π)-sin(0))=π/2 ;  \end{equation} 

Полученный результат иллюстрируется на рис .14.1

                     
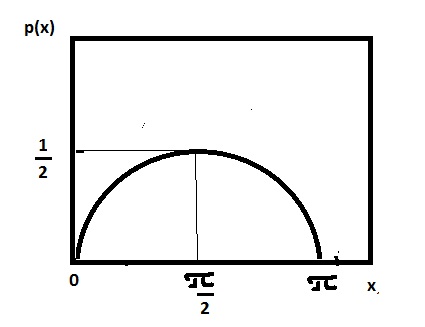
                                                                    Рис.14.1

Математическое ожидание равно среднему значению случайной величины на отрезке \([0,π]\)

2. Дисперсия случайной величины.

Возможны ситуации, когда математические ожидания двух случайных величин совпадают, а рассеяние значений случайной-величины относительно математического ожидания существенно различаются /см.рис 14.2/

                                              среднее    ¯x¯   

-------------------------------------x--------x--------x-----*------x----------x------x---------------------------

                                     x₁         x₂        x₃            x₄           x₅      x6

                                                     ¯x¯   

-------------------------------------x--------x------*--x-----------x-------------------------------------------

                                     x₁         x₂        x₃            x₄          

Возникает необходимость введения дисперсии.

Дисперсией случайной величины X называют математическое ожидание квадрата отклонения случайной величины от её математического ожидания:

\(D(x)=M[x - M(x)]^2\)

Если обозначить математическое ожидание случайной величины как , то формула для вычисления дисперсии имеет вид:

a/для дискретной случайной величины

 \begin{equation} D(x)=\sum\limits_{i=1}^n p_{i}·(x_{i}-m)^2=p_{1}·(x_{1}-m)^2+p_{2}·(x_{2}-m)^2+...+p_{n}·(x_{n}-m)^2  \end{equation}

б/ для непрерывной случайной величины

 \begin{equation} D(x)=\int\limits_{-∞}^{∞}(x_{i}-m)^2·p(x)\,dx ;  \end{equation} 

3.Свойства дисперсии

 a)                    \(D(x)=M[x - M(x)]^2\)=\(M[(x - a)^2]\) \(-\) \([M(x) - a]^2\)

или          \(D(x)=M[x - a)^2] - (m-a)^2\),

где \(a\)- произвольное число.

Если \(a =0\), то из последнего равенства прлучаем, что дисперсия случайной величины равна разности между математическим ожиданием квадрата случайной величины и квадратом математического ожидания: 

 \(D(x)=M(x^2) - M^2(x)\)

б/ Дисперсия суммы независимых случайных величин x и y равна сумме их дисперсий:

\(D(x+y)=D(x)+D(y)\)

4. Среднеквадратическим отклонением случайной величины называется величина

\(σ(x)=(D(x))^{1/2}\)

Пример 3.Случайная величина X задана следующим законом распределения

Определить математическое ожидание, дисперсию, среднеквадратическое отклонение.

Решение.

 1) 

\begin{equation} M(x)=\sum\limits_{i=1}^n x_{i}p_{i}=2·0,3+3·0,4+4·0,3=3; m=3  \end{equation}

 2)

\begin{equation} D(x)=\sum\limits_{i=1}^n p_{i}·(x_{i}-m)^2=0,3·(2--3)^2+0,4·(3-3)^2+0,6·(4-3)^2=0,6  \end{equation}

3)

\(σ(x)=(D(x))^{1/2}=\sqrt{0,6}=0,77\)

Пример 4. Найти дисперсию и среднеквадратическое отклонение случайной величины, плотность распределения вероятностей которой дана. 

Дана плотность вероятности непрерывной случайной величины x :

                     0, x<0

р(x) =            0,5· sinx ,     0≤x≤π

                     0 ,  x>π

Решение. 

1) \(M(Cx)=m=π/2\),

 2) Воспользуемся формулой

\(D(x)=M(x^2) - M^2(x)\)

Получим / два раза интегрируем по частям /:

<

\(M(x^2)=\int\limits_{-∞}^{∞}x^2·p(x)\,dx=0,5\int\limits_{0}^{π}x^2·sin(x)\,dx=- 0,5\int\limits_{0}^{π}x^2 \,dcosx=\)

\(=- 0,5x^2cos(x)|_{0}^{π}-\int\limits_{0}^{π}cos(x)\,dx^2=\)

\(=- 0,5[-π^2-2\int\limits_{0}^{π}x\,dsinx]=\)

\(=- 0,5[-π^2- 2xsin(x)|_{0}^{π} +2\int\limits_{0}^{π}sin(x)\,dx]=0,5 (π^2-4)\)

 Окончательно

\(D(x)=M(x^2) - M^2(x)=0,5 (π^2-4)-\frac{π}{2}=\frac{π^2}{4} -2 \)

\(σ(x)=\sqrt{D(x)}=\sqrt{\frac{π^2}{4} -2 }=0,69\)

Пример 5. Найти математическое ожидание и дисперсию дискретной случайной величины \(x\) распределенной по биноминальному закону.

Решение. Вероятность появления m раз события в серии из m независимых испытаний, если вероятность появлений его в отдельном испытании равна р  , определяется формулой Бернулли

Доказывается, что математическое ожидание такого распределения

\(P_{n}(m)=C_{n}^mp^mq^{n-m}\)

равно

\(M(x)=\sum\limits_{i=0}^np_{m_{i}}(m_{i})=npq\)
Дисперсия равна

 \(D(x)=npq\)