Демоверсия ЕГЭ 2019-2021 по математике. Профильный уровень. Реальный экзамен и демоверсии.
ЕГЭ 2020 по математике Профильный уровень (Дальний Восток)








ЕГЭ 2019 по математике. Профильный уровень.

1.Поезд отправился из Санкт-Петербурга в 23 часа 50 минут (время московское) и прибыл в Москву в 7 часов 50 минут следующих суток. Сколько часов поезд находился в пути?
2.На рисунке точками показана средняя температура воздуха в Сочи за каждый месяц 1920 г. По горизонтали указаны номера месяцев; по вертикали — температура в градусах Цельсия. Для наглядности точки соединены линией. Сколько месяцев средняя температура был
3.На клетчатой бумаге с размером клетки 1 см 1 см изображён треугольник. Найдите его площадь. Ответ дайте в см2.
4.В сборнике билетов по биологии всего 25 билетов. Только в двух билетах встречается вопрос о грибах. На экзамене школьнику достаётся один случайно выбранный билет из этого сборника. Найдите вероятность того, что в этом билете будет вопрос о грибах.
5.Найдите корень уравнения 5 3 81 x
6.Треугольник ABC вписан в окружность с центром O. Угол BAC равен 32 .Найдите угол BOC . Ответ дайте в градусах.
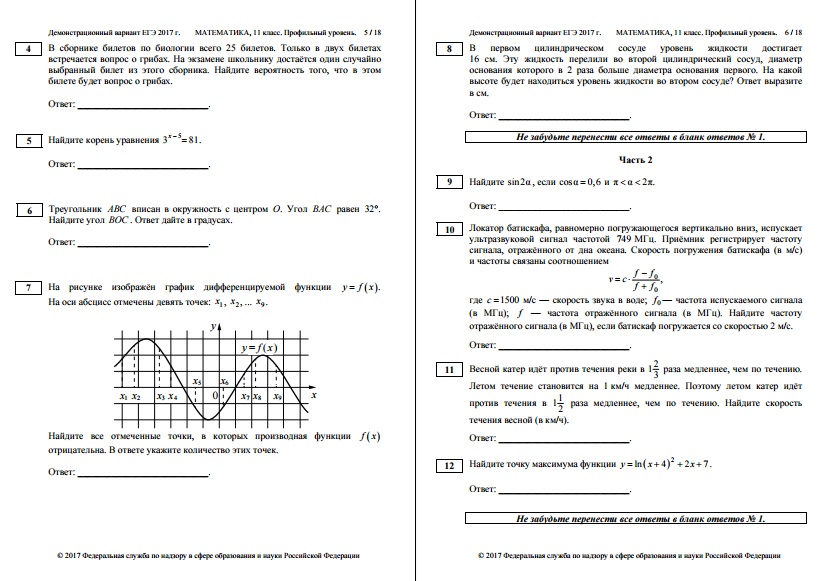
7.На рисунке изображён график дифференцируемой функции y = f( x). На оси абсцисс отмечены девять точек: 1x , 2 x , ... 9 x .Найдите все отмеченные точки, в которых производная функции f x отрицательна. В ответе укажите количество этих точек.
8. В первом цилиндрическом сосуде уровень жидкости достигает 16 см. Эту жидкость перелили во второй цилиндрический сосуд, диаметр основания которого в 2 раза больше диаметра основания первого. На какой высоте будет находиться уровень жидкости во втором со
10.Локатор батискафа, равномерно погружающегося вертикально вниз, испускает ультразвуковой сигнал частотой 749 МГц. Приёмник регистрирует частоту сигнала, отражённого от дна океана. Скорость погружения батискафа (в м/с) и частоты связаны соотношением 0 0
11. Весной катер идёт против течения реки в 213 раза медленнее, чем по течению. Летом течение становится на 1 км/ч медленнее. Поэтому летом катер идёт против течения в 112 раза медленнее, чем по течению. Найдите скорость течения весной (в км/ч).
12.Найдите точку максимума функции \(y=ln(x+4)^2 +2x +7\).
13. а) Решите уравнение \(cos2x= 1 - cos( \frac{π}{2} - x)\) . б) Найдите все корни этого уравнения, принадлежащие промежутку \(5π\) ; \(π 2\)
14. Все рёбра правильной треугольной призмы ABCA1B1 C1 имеют длину 6. Точки M и N — середины рёбер AA1 и A1 C1 соответственно.а) Докажите, что прямые BM и MN перпендикулярны.б) Найдите угол между плоскостями BMN и ABB1.
15.Решите неравенство \(\frac{9^{ x} -2 \cdot3^{x+1} + 4}{3^x-5}+\frac{2\cdot3^{x+1}-51}{3^x-9} ≤ 3^{x}+5\)
16.Две окружности касаются внешним образом в точке K. Прямая AB касается первой окружности в точке A, а второй — в точке B. Прямая BK пересекает первую окружность в точке D, прямая AK пересекает вторую окружность в точке . C а) Докажите, что прямые AD и B
17. 15-го января планируется взять кредит в банке на шесть месяцев в размере 1 млн рублей. Условия его возврата таковы:
18.Найдите все положительные значения a , при каждом из которых система имеет единственное решение.
19.На доске написано более 40, но менее 48 целых чисел. Среднее арифметическое этих чисел равно 3, среднее арифметическое всех положительных из них равно 4, а среднее арифметическое всех отрицательных из них равно 8. а) Сколько чисел написано на доске? б