14. Все рёбра правильной треугольной призмы ABCA1 B1 C1 имеют длину 6. Точки M и N — середины рёбер AA1 и A1 1 C соответственно.а) Докажите, что прямые BM и MN перпендикулярны.б) Найдите угол между плоскостями BMN и ABB1.
Репетитор по математике в Москве предлагает объяснение14. Все рёбра правильной треугольной призмы A B C A1 B1 C1 имеют длину 6. Точки M и N — середины рёбер AA1 и A1 C1 соответственно.
а) Докажите, что прямые BM и MN перпендикулярны.
б) Найдите угол между плоскостями BMN и ABB1.
Решение. а) Пусть точка H — середина AC .

Пояснения : В части а) используем обратную теорему Пифагора.
В части б) необходимо рассмотреть пирамиду MNA1P и два прямоугольных треугольника, которые являются ее гранями PA1M (с прямым углом P и углами 30 и 60 градусов) и NPA1 (c прямым углом A1)
Можно показать, что MN=\(\sqrt{18}\)
Ответ: б) \(arcsin \sqrt{\frac{3}{8}}\)
Другая задача №14. Репетитор по математике в Москве предлагает объяснение.
Ребро SA пирамиды SABC перпендикулярно плоскости основания ABC.
а) Докажите, что плоскость, проходящая через середины рёбер AB, АС и SA, отсекает от пирамиды SABC пирамиду, объём которой в 8 раз меньше объёма пирамиды SABC.
б) Найдите расстояние от вершины А до этой плоскости, если SA = 2√5, AB = АС = 10, BC = 4√5 .
Решение. Репетитор по математике в Москве предлагает объяснение.
а) Объем пирамиды равен произведению основания на высоту и разделить на три. Объем пирамиды
Объем пирамиды \(SABC\)
\(V_{0}=\frac{1}{3}S_{0}H_{0}\)
Объем пирамиды \(FADK\)
\(V_{1}=\frac{1}{3}S_{1}H_{1}\)
\(S_{0}\)
\(S_{1}\)
Из треугольника ABC \(AB=AC=10\) \(BG= GC=2\sqrt{5}\)
Из подобия треугольников \(ABC\) и \(ADK\) и равенства \(AD=BG\) и \(AK=KC\) следует, что
\(DK=2\sqrt{5}\)
Из теоремы Пифагора находим высоту основания ABC \(AG\) основной пирамиды \(SABC\) и основания ADK \(AO\) пирамиды \(FADK\)
\(H_{0}=AG=\sqrt{80}\)
\(H_{1}=AG/2=AO=\frac{\sqrt{80}}{2}\)
Имеем
Объем пирамиды \(SABC\)
\(V_{0}=\frac{1}{3}S_{0}H_{0}\)
Объем пирамиды \(FADK\)
\(V_{1}=\frac{1}{3}\frac{S_{0}}{4}\frac{H_{0}}{2}\)
\(\frac{V_{0}}{V_{1}}=8\)
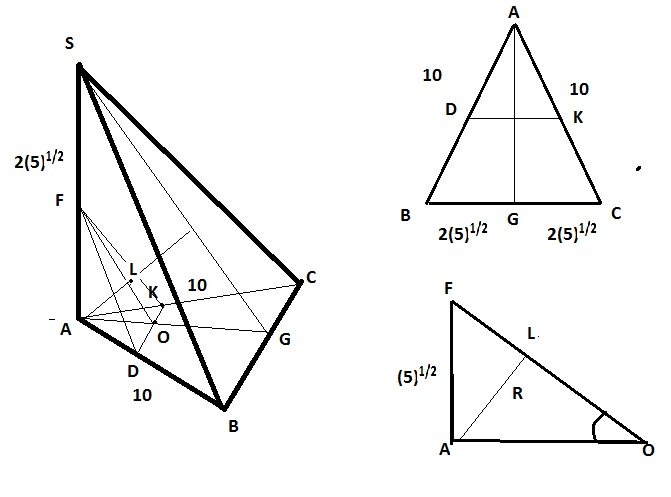
рис.14.2
Репетитор по математике в Москве предлагает объяснение.
б) Из прямоугольного треугольника \(AFO\) с катетами \(FA=\sqrt{5}\) \(AO=\frac{\sqrt{80}}{2}\)
используя теорему Пифагора находим гипотенузу \(FO=5\) .
Из прямоугольного треугольника \(AOL\) следует,
что искомое расстояние \(AL=2\).
Ответ :(от репетитора по математике в Москве) расстояние до указанной плоскости равно 2.
Дана правильная четырехугольная пирамида MABCD с основанием ABCD, стороны основания которой равны 5 √ 2. Точка L - середина ребра MB. Тангенс угла между прямыми DM и AL равен √ 2 .
а) Пусть О - центр основания пирамиды. Докажите, что прямые AO и LO перпендикулярны.
б) Найдите высоту данной пирамиды.
Решение: Пояснения от репетитора по математике ЕГЭ Быстрова Александра.
Трудность этой задачи состоит в том, что трудно найти треугольник , тангенс угла которого составляет 5 √ 2.
Делаем: 1) Строим параллелограм DMNC DM=NC.
2)Продолжаем отрезок AL до AM
3)Видим , что линия ALN есть диагональ прямоугольника ABNM
4) Соединяем точки N и C / Получаем треугольник ANC , в котором линия LO -средняя линия. Угол NCA=90град.
из знания тангенса угла 5 √ 2 и AC =5 находим NC= 10/√ 2.
5) Из треугольника DMO с прямым углом MOD находим искомую высоту МО=5. Ответ 5. 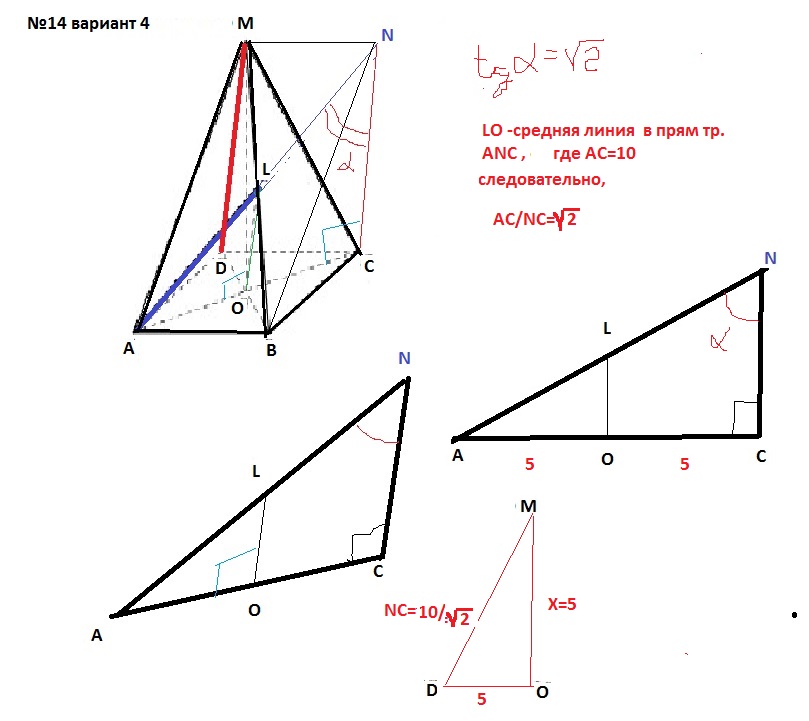
Второй способ:
B правильной треугольной пирамиде SABC с вершиной S все ребра которой равны 6, точка М - середина ребра BC, точка О - центр основания пирамиды, точка F делит отрезок SO в отношении 1:2, считая от вершины пирамиды. Найдите угол между плоскостью MCF и плоскостью ABC.
Найдите отношение в котором плоскость СМF делит отрезок SA , считая от вершины S.
Решение: Треугольник ОМF- прямоугольный, т.к. высота SO пирамиды перпендикулярна ее основанию, значит, и любой прямой, проходящей через точку О.
Для ответа на вопрос задачи нужно найти стороны треугольника FMO.
О - центр вписанной (и описанной) в правильный треугольник окружности.
ОМ - радиус вписанной окружности
r=a/(2•√3)⇒
OM=[(6√3):2]:3
После сокращений получаем ОМ=√3
FO= 2/3 SO, т.к. SF:OF=1:2
SO найдем из ⊿ SOB
ВО - радиус описанной окружности и вдвое больше радиуса вписанной окружности:
ВО=2√3
SO=√( SB²-BO² )=√24 ⇒
FO=(√24):3•2 =[√(3•4•2)]:3•2 после сокращений получим
FO=(4√2):√3
tg FMO=FO:OM=(4√2):3, что по таблице соответсвует углу ≈ 62º3'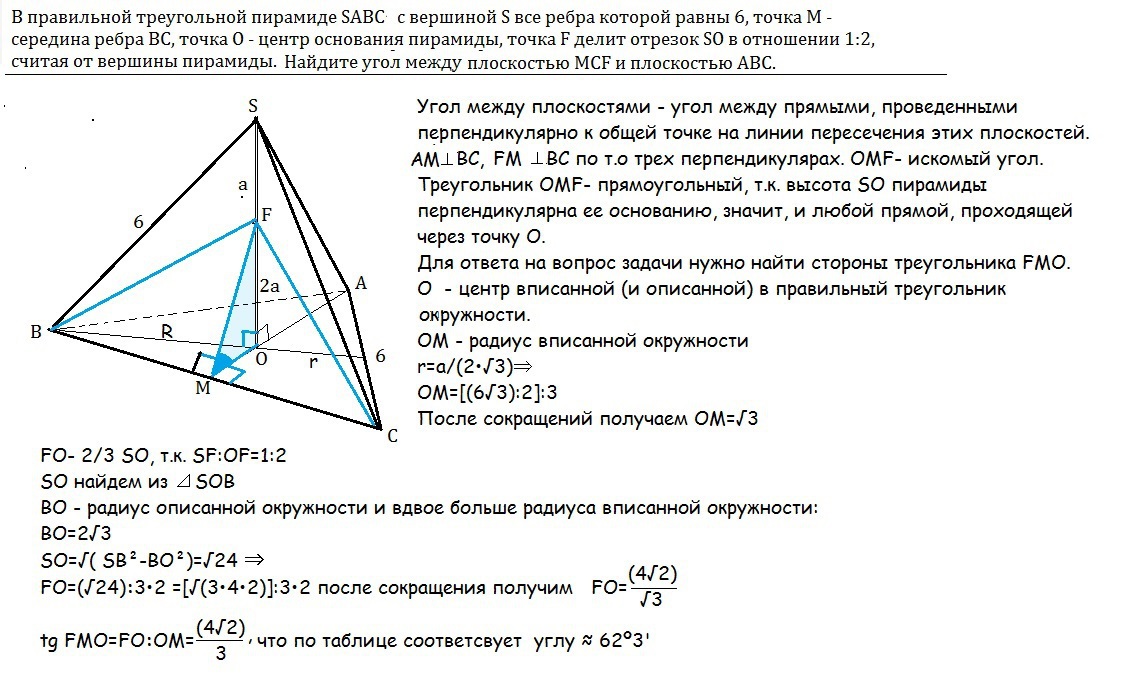
Найти отношение в котором плоскость СМF делит отрезок SA , считая от вершины S:
рассмотрим треугольник SAM. В нем SO-высота, SA=6, MO=√3, а ОА=2ОМ=2√3.
Можно показать, что в этом треугольнике MFK перпенд. SA
Задача №14.
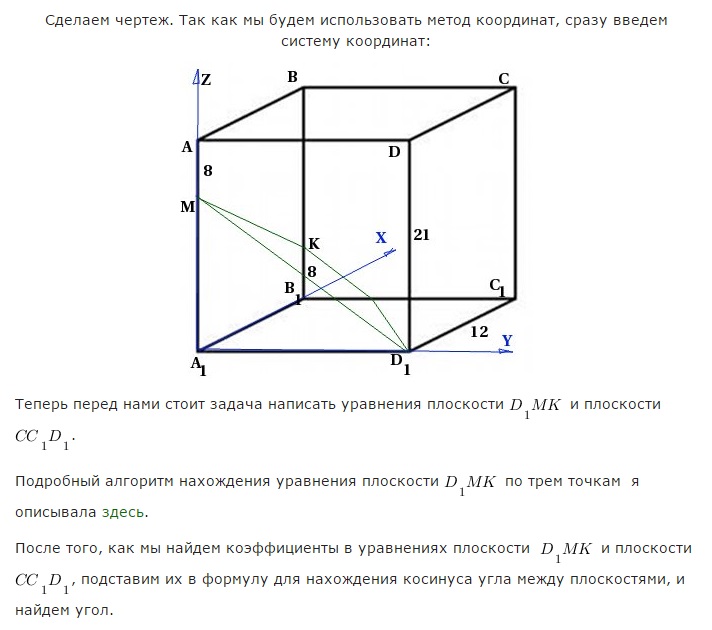
В правильной четырехугольной призме ABCDA_1B_1C_1D_1 со стороной основания 12 и высотой 21на ребре AA_1 взята точка М так, что AM=8.
На ребре BB_1 взята точка K так, что B_1К=8.
Найдите угол между плоскостью D_1MK и плоскостью CC_1D_1.