§13. Интегральные характеристики случайной величины. Функция распределения

Допустим, нас интересует вероятность не какого-нибудь конкретного значения случайной величины X , а вероятность того,что случайная величина примет все возможные значения до какого-то значения х₀ ,то есть ℜ( х₀<Х) . Чтобы найти эту вероятность нужно про-

суммировать все значения вероятностей до х₀<Х в случае дискретной случайной величины или проинтегрировать в случае непрерывной случайной величины. Получается интегральная величина, которая называется функцией распределения. Дадим строгое определение.

Определение. Вероятность того, что случайная величина X примет значение меньшее х₀, называется функцией распределения случайной величины о обозначается:

                                 F(x) =ℜ(х₀<Х)

1. Для непрерывной случайной величины , закон распределения которой определяется плотностью распределения вероятностей р(*) , функция распределения  равна:

\begin{equation} F(x)=\int\limits_{-∞}^{x}p(x)\,dx \end{equation}

Очевидно, что функция распределения и плотность распределения вероятностей непрерывной случайной величины связаны равенством:

\begin{equation} F^{,}(x)=p(x) \end{equation}

2. Для непрерывной случайной величины заданной законом распределения:

функция распределения равна -

\begin{equation} \sum\limits_{x_{i}<x_{k}}^x  p_{x_{i}}=p_{1}+p_{2}+...+p_{n} =1 \end{equation}

3. Свойства функции распределения

1. На левой границе значений случайной величины x<-∞

вероятность обращается в нуль, поэтому 

F(-∞) =ℜ(х<-∞)=0

2. На правой  границе значений случайной величины X > + -∞ событие является достоверным, т.е.

F(+∞) =ℜ(х<+∞)=1

3. Исходя из возможных значений вероятностей, имеем

 \begin{equation} 0≤F(x)≤1 \end{equation}

4. По смыслу функции распределения случайной величины, суммирующей все значения до X , выполняются следующие неравенства, при х₁<x₂

получим

 \begin{equation}F(x_{1})≤F(x_{2}) \end{equation}

так как

      \begin{equation}ℜ(x_{1})≤ℜ(x_{2}) \end{equation}

 то есть функция \(F(x)\) является неубывающей.

5. Вероятность того, что значения случайной величины удовлетворяет

 условию

 \begin{equation}x_{1}≤x<x_{2}, \end{equation}

равна

 \begin{equation}ℜ(x_{1}≤x<x_{2})=F(x_{2})- F(x_{1})=\int\limits_{x_{1}}^{x_{2}}p(x)\,dx\end{equation}

6.Графически функция распределения дискретной случайной

определяется многоугольником распределения /рис. 13.1 /

\begin{equation} \sum\limits_{i=1}^4  p_{x_{i}}=p_{1}+p_{2}+...+p_{n} =1 \end{equation}

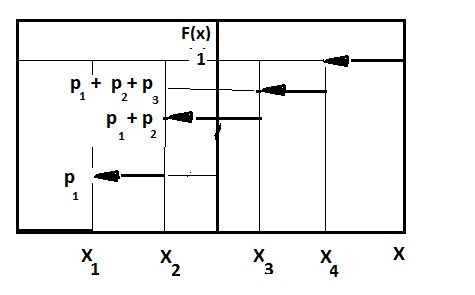
                                                    рис.13.1

7.Непрерывная случайная величина определяется плотностью распределения вероятностей (например,рис. 13.2) p(x)

 \begin{equation} \int\limits_{-∞}^{∞}p(x)\,dx =1 \end{equation}

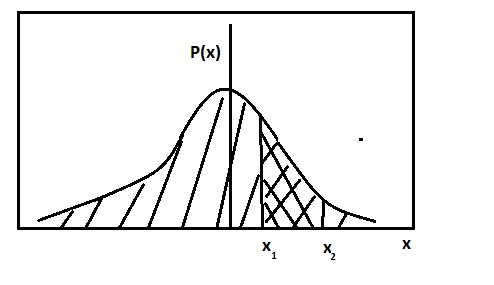
                                                    рис. 13.2

Площадь области под графиком распределения \(p(x)\) равна 1.

График функции распределения в этом случае имеет вид (рис. 13.3)

                                                    рис. 13.3

Вероятность случайной величине принять значения в промежутке \(x_{1}≤x<x_{2}\) равна: 

 \begin{equation} F(x_{2})- F(x_{1})=\int\limits_{x_{1}}^{x_{2}}p(x)\,dx\end{equation}

и равна площади фигуры с двойной штриховкой на рис.13.2

Пример I.Монета подбрасывается 5 раз. Написать закон распределения случайной величины равной числу выпавших орлов. Построить многоугольник распределения и функцию распределения. Найти F(2) ; вероятность попадания случайной величины в интервал 2 < X < 4.

Решение. Случайная величина X - число выпавших орлов может принять следующие значения:

Вероятности выпадения орла определяются формулой Бернулли, получим:

   р₅(0) = C₅⁰ (1/2)⁰(1/2)⁵ = 1/32 ;

  р₅(1) =C₅¹ · (1/2)¹(1/2)⁴ = 5/32 ;

  р₅(2) =C₅²· (1/2)²(1/2)³ = 10/32 ;

  р₅(3) =C₅³· (1/2)³(1/2)² = 10/32 ;

  р₅(4) =C₅⁴· (1/2)⁴(1/2)¹ = 5/32 ;

  р₅(5) =C₅⁵ · (1/2)⁵(1/2)⁰ = 1/32 ;

 I) Закон распределения имеет вид:

\begin{equation} \sum\limits_{i=1}^5  p_{x_{i}}=p_{1}+p_{2}+...+p_{5} =1 \end{equation}

 2)Многоугольник распределения

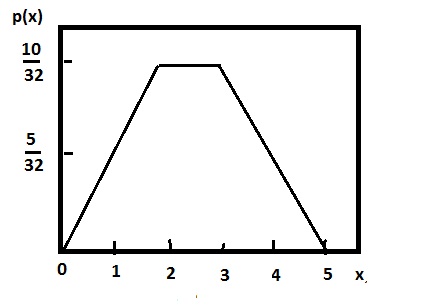
рис. 13.4

 3) Функция распределения F(x)

                       0,                                                       если x≤0

F(x)=               1/32,                                                    0<x≤1

                        1/32 +5/32 =6/32 ,                              1<x≤2 

                        1/32 +5/32 +10/32=16/32 ,                   2<x≤3

                        1/32 +5/32 +10/32+10/32=26/32 ,         3<x≤4   

                       1/32 +5/32 +10/32+10/32+5/32=31/32 , 4<x≤5

                        1/32 +5/32 +10/32+10/32+5/32+1/32=1 , 5≤x

 4) F(2)=? Это вероятность того, что случайная величина примет значение меньшее, чем 2, то есть 

            F(2)=P(x<2)

В этом случае случайная величина может принять значение О и I. Поэтому

            F(2)=P(x<2)=р₅(0)+ р₅(1)=1/32+5/32 =6/32

5)    2<x≤4   . Вероятность такого события равна:

P(2<x≤4 )=F(4)-F(2)=  р₅(0)+ р₅(1)=(р₅(0)+р₅(1)+р₅(2)+р₅(3))-(р₅(0)+р₅(1)) =20/32

 т.е. случайная величина может принять два значения 2 и 3.

Пример 2. Случайная величина x задана на всей числовой оси функцией распределения:

       F(x)= (1/2)  +  (1/π)·arctg x

 Найти функцию плотности вероятности и вероятность того,

что случайная величина x  примет значение заключенное в интервале  (0,1) .

Решение. I. По определению плотность вероятности P(x) равна производной от функции распределения:

P(x)=(F(x))'

(F(x))'= ((1/2)  +  (1/π)·arctg x) =0+ (1/π)·(arctg x)'=(1/π)·(1/(1+x²))

2. Вероятность случайной величине быть в интервале (0,1)

равна: 

P(0<x≤1 )=F(1) - F(0)= (1/π)·(arctg 1    - arctg 0  ) =1/4

или

 \begin{equation} P(0<x≤1 )=\int\limits_{0}^{1}p(x)\,dx=\int\limits_{0}^{1}\frac{1}{1+x^2}=F(1) - F(0)   \end{equation}