2. Решение второй задачи предлагает олимпиадный репетитор по математике и физике

2. Найдите главный (наименьший положительный) период функции

\(y=(arcsin(sin((arccos(cos4x))))^{-5}\)

Ответ: \(\frac{π}{4}\).

Решение предлагает олимпиадный репетитор по математике и физике:

1) Число \(\frac{2π}{4}\) является периодом функции \(cos4x\) .

2)Так как множество значений функции

\(z= arccos(cos t)\) равно \([0;π]\)  ,

3) а функция \(arcsin(sinz)=z\) , при \([0,\frac{π}{2}]\)  

функция \(arcsin(sinz)=π-z\) , при \([\frac{π}{2},π]\)

 4)   то  \(\frac{π}{4}\)  будет периодом функции y. 

5)Так как точки вида \(\frac{Nπ}{4}\) , \(N∈ Z\)

не принадлежат области определения функции \(y\), то \(\frac{π}{3}\) – наименьший период.

Ответ : \(\frac{π}{4}\) .
Построение графиков

\(arcsin(sinz)=z\) 


Построение графика \(y=(arcsin(sin((arccos(cos4x))))^{+1}\)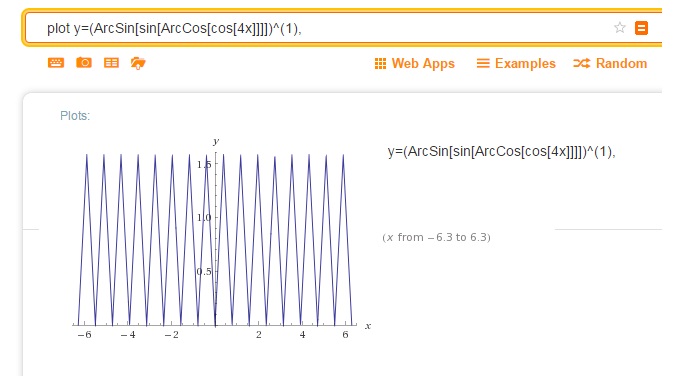


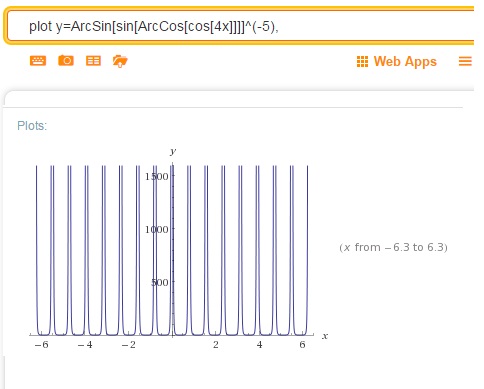
Построение графика \(y=(arcsin(sin((arccos(cos4x))))^{-5}\)  

           
 

Олимпиада Ломоносов по физике.  Задачи 11 класс. 
Решение олимпиады по физике  Ломоносов (1 тур) предлагает олимпиадный репетитор по математике и физике
Решение олимпиады по физике  Ломоносов (2 тур) предлагает олимпиадный репетитор по математике и физике