1.Алгебра событий. Теория вероятностей. Примеры

Глава I. Теория вероятностей

Курс репетитора по теории вероятности репетитора Быстрова Александра Анатольевича.

§1 Алгебра событий.

Теория вероятностей - математическая наука, изучающая закономерности в массовых случайных явлениях. Например, бросается монета. При одном бросании мы не можем сказать заранее, что выпадет: орел или решетка. Но если монету бросать много раз, то число выпадений орла или решетки будет примерно одинаково. В этом и проявляется статистическая закономерность,. Теперь нужно найти её численное выражение.

Пример. Допустим, что монета бросается 100 раз. 48 раз выпал орел и 52 раза выпала решетка. В этом случае говорят, что вероятности выпадения орла и решетки одинаковы и равны 0,5 ,т.е.

\begin{equation}\begin{split} P = \frac{48}{100}\approx\frac{52}{100}\approx\frac{1}{2}\end{split} \end{equation}

Таким образом, наличие большого числа более или менее однотипных явлений приводит к возникновению закономерностей, проявляющихся - тем сильнее, чем больше та серия опытов, которая рассматривается.

В теории вероятностей основную роль играет понятие события.

Событием называется всякое явление, относительно которого имеет смысл говорить произошло оно или нет.

Случайные события обозначаются буквам А, 3, С, Д и т.д. Например, А - появление орла при бросании монеты, 3 - выпадение ‘решетки.

Различные события, происходящее при реализации данного комплекса условий, могут быть связаны между собой определенными соотноше- ниями. “

1. Если при каждом осуществлении данного комплекса условий,при  котором наступает событие А, наступает и событие В, то говорят, что А влечет В и пишут А с В / или В принадлежит А /.

Например, при бросании игральной кости / кубик с одинаковыми гранями, на которых нанесены цифры от I до 6 / событие "выпала двойка" влечет за собой понятие "выпало четное число очков".

2. Если А влечет В и в то же время В влечет А, то событие А и В называют равносильными и пишут А=В.

3. Суммой A + В двух событий А и В называется событие, состоящее в появлении хотя бы одного из них,т.е. А или В , или их обоих вместе.

Пример.I. Если событие А состоит в попадании точки внутрь крута А, а В - внутрь круга В, то.суммой А + В будет заштрихованная область.

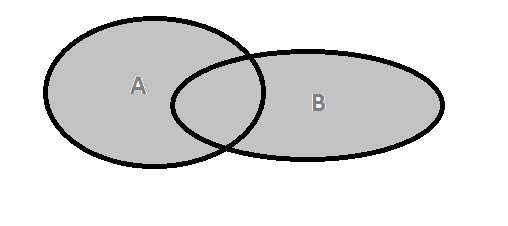
Рис.1

4. Произведением АВ двух событий А и В называется событие состоящее в совместном появлении и события А и события В. Заштри- хованная область на рис.2

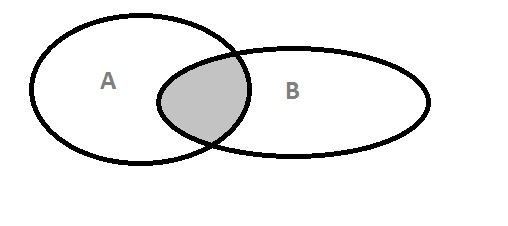
Рис.2

Определение произведения и суммы событий очевидным образом обобщается на случай любого числа событий.

5. Событие, состоящее в том, что событие А происходит, а событие В не происходит, называется разностью событий А и В и обозначается А - В. Заштрихованная область на рис.З

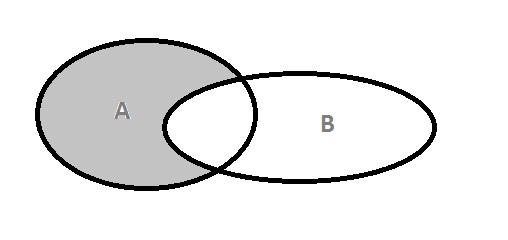
Рис.З

б. Если А - событие, то событие состоящее в том, что А не наступило, называется противоположным А и обозначается \(\bar{A}\) Например, если А - выпадение четного числа очков, то \(\bar{A}\) выпадение нечетного числа очков.

7. Событие называется достоверным, если оно обязательно происходит при реализации данного комплекса условий. Будем обозначать достоверное событие буквой \(E\).

8. Событие называется невозможным \(N\) , если оно не может произойти ни при одной реализации данного комплекса условий. Например, при бросании одной игральной кости не может выпасть число большее 6.

9. Любые противоположные события А и \(\bar{A}\) связаны между собой

\(А +\bar{A}=Е\) ; \(А\bar{A}=N\)

10. События А и В называются несовместимыми, если их одновременное наступление невозможно,т.е.

\(AB=N\)

11. События \(В_{1}, В_{2}, . . ., В_{n}\) называются попарно несовместимыми, если

\(В_{i}В_{j}=N\) \(i≠j\)

Если \(А = В_{1}+В_{2}+В_{n}\) и события \(В_{i}\) попарно несовместимы, то говорят, что событие Л подразделяется на частные случаи

\(В_{i}, i=1,2,...n\)

12. Говорят, что события \(В_{1}, В_{2}, . . ., В_{n}\) образуют полную группу, если хотя бы одно из них должно обязательно наступить,т.е. \(В_{1}+ В_{2}+ . . .+ В_{n}=E\)

13. Говорят, что события \(В_{1}, В_{2}, . . ., В_{n}\) образуют полную группу попарно несовместимых событий , если

\(В_{1}+ В_{2}+ . . .+ В_{n}=E, В_{i}В_{j}=N, i ≠ j\)

14. Совокупность всех случайных событий, которые могут наступить при реализации данного комплекса условий называется полем событий \(S\).

Если полю событий принадлежат события \(А\) и \(В\) , то ему принадлежат также события \(АВ, А + В, А - В,\) достоверное событие Е и невозможное.

Пример. По мишени производится три выстрела. Рассматривается-событие А - попадание при 1-м выстреле / I = 1,2,3 /.

Представить следующие события:

I. А - все три попадания.

2. В - все три промаха.

3. С - хотя бы одно попадание.

4. Д - хотя бы один промах.

5. Z- не меньше двух попаданий.

6. F - не больше одного попадания.

7. G - попадание в мишень не раньше, чем при третьем выстреле. Решение.

I. \(A=A_{1}A_{2}A_{3} \),

2. \(В=\bar{A_{1}}\bar{A_{2}}\bar{A_{3}}\)

3. \(С= A_{1}+A_{2}+A_{3}\) ,

или \(С=A_{1}+\bar{A_{1}}A_{2}+\bar{A_{1}}\bar{A_{2}}A_{3}\),

или

\(С=A_{1}\bar{A_{2}}\bar{A_{3}}+\bar{A_{1}}A_{2}\bar{A_{3}}+A_{1}\bar{A_{1}}\bar{A_{2}}A_{3}+A_{1}\bar{A_{2}}A_{3}+\bar{A_{1}}A_{2}A_{3}+A_{1}A_{2}\bar{A_{3}}\),

4. \(D= \bar{ A_{1}}+ \bar{A_{2}}+ \bar{A_{3}} \).

5. \(Z=\bar{A_{1}}A_{2}A_{3} +A_{1}\bar{A_{2}}A_{3} +A_{1}A_{2}\).

6. \(F=\bar{A_{1}}A_{2}\bar{A_{3}}+A_{1}\bar{A_{2}}A_{3}+\bar{A_{1}}\bar{A_{2}}\)

7. \(G=\bar{A_{1}}\bar{A_{2}}\).

 ///////