Задача: Пловец переплывает реку шириной L по прямой, перпендикулярной берегу,
и возвращается обратно, затратив на весь путь время t1 = 4 мин.
Проплывая такое же расстояние L вдоль берега реки и возвращаясь обратно,
пловец затрачивает время t2 = 5 мин.
Во сколько n раз скорость пловца относительно воды превышает скорость течения реки.

Решение: 
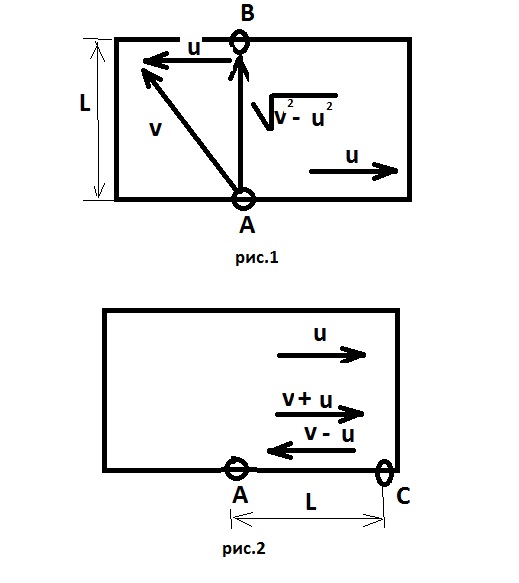
На рис.1 и рис.2 показаны схемы движения пловца поперек реки и вдоль реки соответственно.
Вектор скорости пловца \(v\) на рис.1 направлен под некоторым углом к берегу, так как течение реки сносит его. 
Скорость течения реки \(u\).
Результирующий вектор скорости движения пловца поперек реки равен \(\sqrt{v^2-u^2}\)
Важно понимать, что при движении пловца вдоль реки результирующая скорость пловца по течению равна \(v+u\), а против течения реки скорость результирующая  равна \(v-u\)

Составим систему уравнений:

1) для движения пловца вдоль реки (рис.2)
  \(\frac{L}{v+u}+\frac{L}{v-u}=t_{2} =\frac{5}{1}\)

2) для движения пловца поперек реки (рис.1)

\(\frac{2L}{\sqrt{v^2-u^2}}=t_{1} =\frac{4}{1}\)

или

3) \(\frac{1}{v+u}+\frac{1}{v-u}=\frac{5}{L}\)

4) \(\frac{2}{\sqrt{v^2-u^2}}=\frac{4}{L}\)

Ответ: \(n=\frac{t_{2}}{\sqrt{t_{2}^2-t_{1}^2}}\)