Решение задач
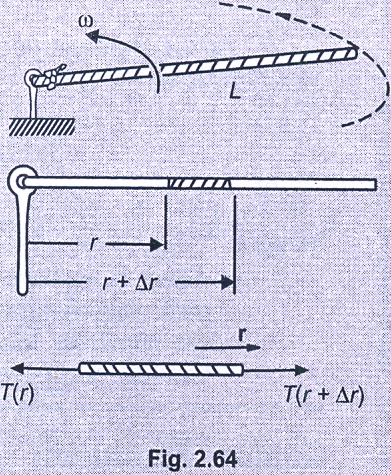
Однородная веревка массы M и длиной L поворачивается на одном конце и кружится с равномерной угловой скоростью $\omega$ . Найти напряжение в канате на расстоянии $r$ от оси?
1.Задача:Однородная веревка массы \(M\) и длиной \(L\) поворачивается на одном конце и кружится с равномерной угловой скоростью \(\omega\) . Найти напряжение в канате на расстоянии \(r\) от оси? Пренебрежение тяжести.
Решение:
2. Соответствующее уравнение
\[\vec{F}=m\vec{a}\]
3. Рассмотрим дифференциальный элемент, как показано на рисунке.

Я рассматривал установку напряжения, действующего на дифференциальный элемент как таковой, так как считал, что результирующая сила, которая должна быть действующая на дифференциальный элемент должен быть в направлении центростремительного ускорения. Таким образом, мы получаем
\[T+dT-T=(dm)\omega^2x\implies dT=\left(\dfrac{M}{L}\omega^2x\right)dx\]
Интегрирование выражения дает
\[\int^{T}_{T_0}{dT}=\int^{r}_{0}\left({\dfrac{M}{L}\omega^2x}\right)dx \implies T-T_0=\dfrac{M}{2L}\omega^2r^2\]
, интегрирования выражения с соответствующими пределами мы получаем.
Теперь, чтобы найти Теперь, чтобы найти , мы помещаем значение этого , который действует на конце веревки. Значение , т.е. значение напряжения не действующей в направлении, противоположном направлению ускорения элемента мы видим, что значение является как нет напряжение действует в направлении наружу каната. Интегрирования выражения с соответствующими пределами мы получаем \[-T_0=\dfrac{M}{2L}\omega^2L^2\implies T_0=-\dfrac{M}{2L}\omega^2L^2\]
мы помещаем значение этого\[\therefore T=T_0+\dfrac{M}{2L}\omega^2r^2=\dfrac{M}{2L}\omega^2\left(r^2-L^2\right)\]
Ответ, который я получаю имеет противоположный знак, чем книги, которая является
\(\dfrac{M}{2L}\omega^2(L^2-r^2)\).
Это потому, что направление, в котором я считал \(T\) действовать противоположно тому, что я предполагал. Если это так, то не значит, что \(T+dT(\gt T)\)
находится в направлении, противоположном направлению центростремительного ускорения, так как будет центростремительное ускорение подаваться к дифференциальному элементу, если результирующая сила в направлении, противоположном тому, что центростремительной accleration.
Вы определили изменение координаты х, как справа минус левое значение х при определении изменения напряжения в левой величины минус справа. Это дает вам сообщение об ошибке входа.
Но если не увеличение силы тяжести, как мы идем по направлению к центру круга, в котором круг кружится. Есть ли, это просто означает, что выражение
\(dT=\left(\dfrac{M}{L}\omega^2x\right)dx\)
имеем
\(dT=-\left(\dfrac{M}{L}\omega^2x\right)dx\).
Кроме того, я не читал "пренебрежение тяжести" часть вопроса, поэтому я думал, что должно быть минимальная скорость, для которой вся тросовых вращается, т.е. веревка не ослабевать в любом месте во время вращения. И я был не в состоянии придумать способ подойти к этой проблеме, если вы можете предложить, как пытаться это было бы очень полезно.
