Постановка задачи:
Блок- брусок A положили на клин, наклоненной под углом \(θ\). Коэффициент трения между блоком и плоскостью \(μ\). Клин получает горизонтальное ускорение \(a\) . Предполагая, что  \(tg⁡θ>μ\), 
найти минимальное ускорение  блока, чтобы  клин не скользил.

другая похожая задача:
На клин, массой m1, находящийся на горизонтальной поверхности под углом альфа, поместили брусок массой m2. Клин движется вправо с ускорением a1, а брусок скользит вниз по грани с ускорением a2. Найти эти ускорения, при условии, что трение везде отсутствует.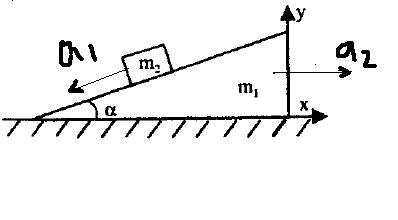

Рещение: 1.Применяется уравнения второго закона закон Ньютона при действии статического трения

2. У нас есть три силы, действующие на блок: нормальная сила, трение и сила тяжести.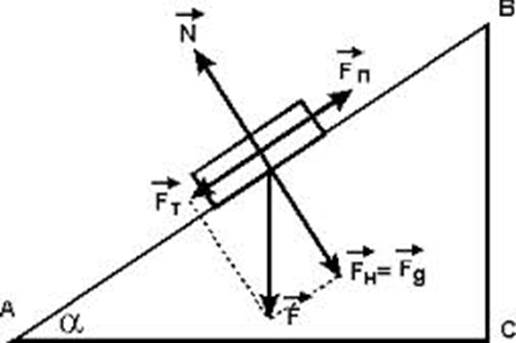



Если мы определяем наши системы координат так, чтобы у-направление и х-направление вниз, то мы имеем следующие уравнения:

y-direction: \(N \sin \theta + f \sin \theta - mg = 0\)
x-direction: \(N \sin \theta - f \cos \theta = ma\)

then
\(N \cos \theta + f \sin \theta = mg\)

Получаем
\(\tan \theta > \mu\)
известно,что \(f = \mu N\)

Тогда
\(N (\cos \theta + \mu \sin \theta) = mg\)
\(N (\sin \theta - \mu \cos \theta) = ma\)

Выражаем ускорение
\(\displaystyle a = \frac{g(\sin \theta - \mu \cos \theta)}{\cos \theta + \mu \sin \theta}\)