Решение задач
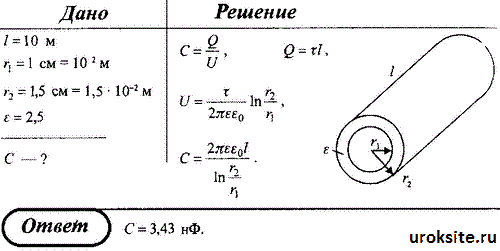
Определить емкость коаксиального кабеля длиной 10 м, если радиус его центральной жилы r1 = 1 см, радиус оболочки r2 = 1,5 см, а изоляционными материалом служит резина (ε = 2,5).
56. Определить емкость коаксиального кабеля длиной 10 м, если радиус его центральной жилы r1 = 1 см, радиус оболочки r2 = 1,5 см, а изоляционными материалом служит резина (ε = 2,5).
Случайная величина X имеет стандартное нормальное распределение (то есть с параметрами a=0 и б^2 = 1). Найти плотность случайной величины Y = X^2. РЕШЕНИЕ. Случайная величина X имеет стандартное нормальное распределение. Следовательно, плотность распределения случайной величины X имеет вид: \(f(x) = (1/sqrt(2П))*e^(-(x^2)/2).\) \( Y = X^2 F(y) = P(Y<y) = P( X^2 <\) y ) Если \(0y<=0\), то F(y) = 0 Если \(y>0\) , то \(F(y) = int_{-sqrt(y)}^{sqrt(y)} f(x)dx = \) \(= (1/sqrt(2П))*int_{-sqrt(y)}^{sqrt(y)} e^(-(x^2)/2) dx \) \(F(y)={0, y<=0 \) \( {(1/sqrt(2П))*int_{-sqrt(y)}^{sqrt(y)} e^(-(x^2)/2) dx, y>0 \) \(g(y) = {0, y<=0 {(1/sqrt(2Пy))*e^(-y/2), y>0\)
