Пример 2: Сферический конденсатор.

Найти электрическую емкость  сферического конденсатора, состоящего из двух концентрических сферических оболочек

с радиусами а и Ь.

.

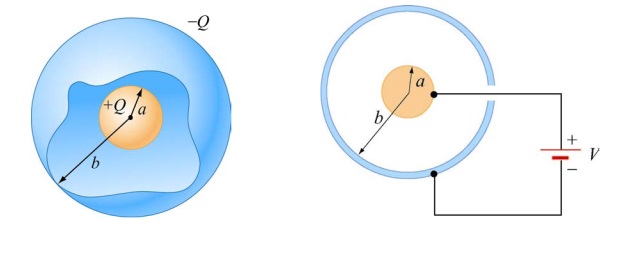
Сферический конденсатор состоит из двух концентрических сферических оболочек с радиусами \(а\) и \(Ь\), как показано на рисунке 2.1а. На рисунке 2.1б показана схема   заряда  конденсатора от ЭДС (батареи питания или аккамулятора). Внутренняя оболочка имеет заряд \(+ Q\) равномерно распределенныq по ее поверхности, а на внешней оболочке, равный, но противоположный по знаку заряд \(-Q\).

                        a                                                                                             b

Рисунок 2.1 (а) Сферическая конденсатор, состоящий из двух концентрических сферических оболочек с радиусами а и Ь.                                                            (b) Заряд сферического конденсатора.

Емкость этой конфигурации может быть вычислена следующим образом:

электрическое поле в области \(а <г <Ь\) задается

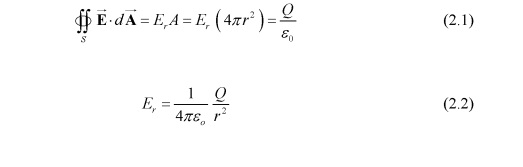
Разность потенциалов между двумя проводящими оболочками:

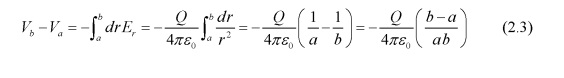
С разностью потенциалов \(AV = V_{a}-V_{b}\), мы имеем 

Изолированный проводник также может иметь емкость. В пределе, где \(b→∞\), приведенное выше уравнение становится

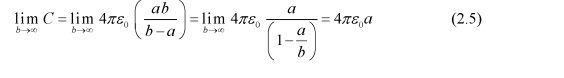
Таким образом, для одного изолированного сферического проводника радиуса R,

емкость равна

(2.6)

Данное выражение можно получить, заметив, что сфера радиуса R имеет потенциал

\(V = \frac{Q}{4πε_{0}}\) и \(V = 0\) на бесконечности. Это дает 

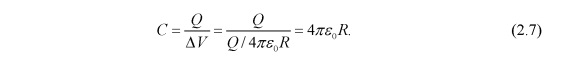
Как и следовало ожидать, емкость изолированной заряженной сферы зависит только от радиуса \(R\).