Решение задач
5.Задачи ЕГЭ профильный геометрия.
§ 5. Решение задач. Геометрия.
Отличительной особенностью любой истинно геометрической задачи является то, что для ее понимания необходим чертеж
Простейшие задачи Следующие формулы геометрии желательно помнить:
площадь треугольника (рис. 2) с полупериметром р и ради¬усами вписанной г и описанной R окружностей1' равна
S = iah = i6сsin Q = рг = ^ = у/р(р - а)(р - Ь)(р - с),
а площади трапеции и параллелограмма равны
S = а ^ ^ ft и S = ah,
где а и 6 — основания, a h — высота;
в прямоугольном треугольнике (рис. 3) с медианой т и вы¬сотой ft, опущенными на гипотенузу с, имеют место следующие ) Остальные обозначения показаны на рис. 2.
a2+b2=c2, а2 — хс, h2 = ху, т = с/2 = R, 2S = ab — ch\
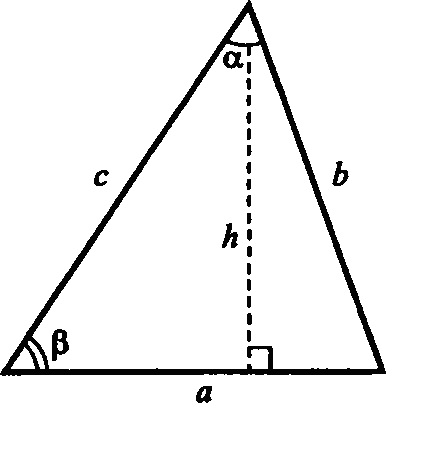
Рис. 2
Рис. 3
площадь четырехугольника с диагоналями d\, дг и углом <р между ними равна
S = |did2sini^;
площадь описанного многоугольника равна
S = рг,
где р — полупериметр многоугольника, г — радиус вписанной в него окружности;
длина окружности и площадь круга радиуса г соответствен¬но равны
С = 2ят и S = кг2.
Пример 1 .
Радиус О А = 10 окружности с центром О делит хорду ВС = 12 пополам. Найти АВ.
Решение.
См. рис. 4: О A _L ВС =>• х = %/Ю2 — 62 = 8 => у = 10 — х = 2 => z = \/у2 + 62 = ...
Ответ: 2\/ТО.
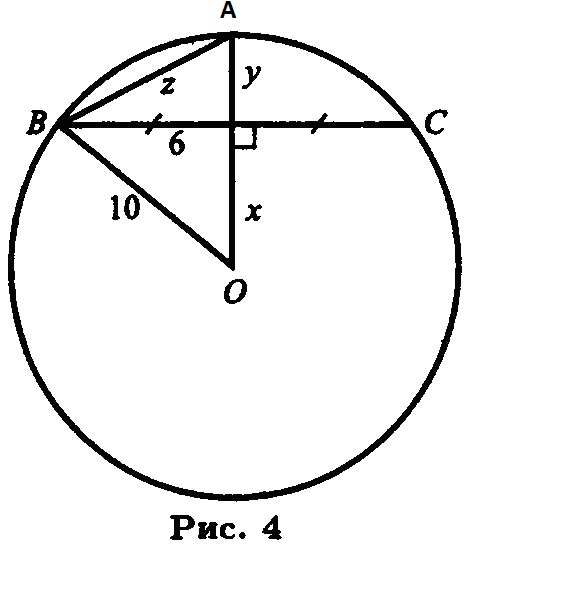
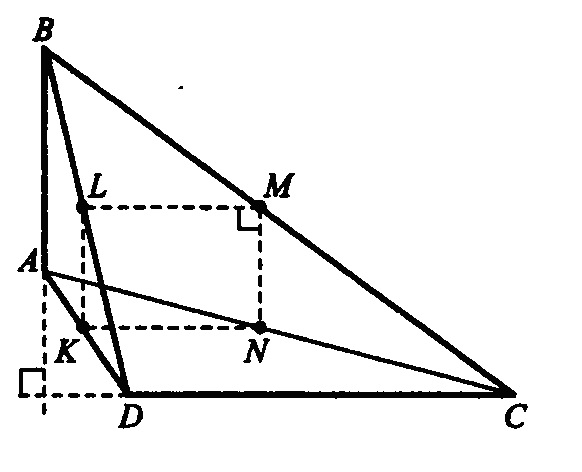
Рис. 5
Некоторые полезные геометрические утверждения не называются теоремами, а разбираются в школьном курсе в виде задач.
Пример 2 . В выпуклом четырехугольнике ABCD от¬резок, соединяющий середины диагоналей, равен отрезку, соединяющему середины сторон AD и ВС. Найти угол между прямыми АВ и CD. Решение. См. рис. 5:
KLMN — параллелограмм, т. к. К, L,M,N — середины отрезков и KL || MN ||
АВ, KN || LM || CD (средние линии в соответствующих треугольниках); 210
КМ — LN =£• KLMN — прямоугольник;
KL ± MN =*- AB 1 CD.
Ответ: 90°.
227° . Найти площадь правильного треугольника, сторона которого равна стороне ромба с диагоналями 10 и 12. А
228°. Найти периметр правильного треугольника, если центр описанной около него окружности удален от хорды, равной 2, на расстояние 3.
229° . В треугольнике АВС основание D высоты CD = VS лежит на стороне АВ. Найти АС, если АВ = 3 и AD = ВС.
211 230°. Найти площадь прямоугольного треугольни¬ка, один из катетов которого равен 13, а высота, опущенная на гипотенузу, равна 12.
212 231. В прямоугольном треугольнике АВС с ги¬потенузой АВ проведены медиана СМ и высота СН, при¬чем точка Н лежит между A is. М. Найти АН : AM, если СМ : СН = 5:4.
232* . Один из углов треугольника равен разности двух других, наименьшая сторона треугольника равна 1, а сумма площадей квадратов, построенных на двух других сторонах, вдвое больше площади описанного около треугольника круга. Найти наибольшую сторону треугольника.
233 . Окружность радиуса л/З, вписанная в прямоугольный треугольник АВС, касается катета АС в точке К. Найти ВК, если А А = 30°.
У/ 234. Окружность радиуса 3, центр О которой лежит на гипотенузе АВ прямоугольного треугольника, каса¬ется катетов. Найти площадь треугольника, если О А = 5.
235 . Окружность, центр которой лежит на гипотенузе АВ прямоугольного треугольника АВС, касается ка¬тетов АС и ВС в точках Е и D соответственно. Найти ZB, если АЕ = 1 и BD = 3..
236 . В треугольнике АВС проведена биссектриса CD прямого угла. Из точки D опущен перпендикуляр DM = = \/3 на сторону АС. Найти ВС, если AD = 2\/3.
237° . На стороне АВ = 4 треугольника АВС с углами ZA = 30° и ZB = 130° как на диаметре построена окруж¬ность. Найти площадь части круга, лежащей внутри треугольника.
238. Две равных хорды окружности образуют вписанный угол величиной 30°. Найти отношение площади части круга, лежащей внутри угла, к площади всего круга.
239*. Точка пересечения двух общих касательных к двум непересекающимся окружностям, меньшая из которых имеет радиус г, лежит на линии их центров на расстоянии 6г от центра большей окружности и делит отрезок касательной между точками касания в отношении 1 : 3. Найти площадь фи¬гуры, состоящей из двух частей, ограниченных касательными и ббльшими дугами окружностей..
240 . Найти площадь выпуклого четырехугольника с диагоналями 3 и 4, если отрезки, соединяющие середины противоположных сторон, равны.
241° . Прямая, параллельная стороне АВ треугольника АВС, пересекает стороны АС и ВС в точках М и N соответственно. Найти AM : СМ, если площадь треугольника MCN вдвое больше площади трапеции AMNB.
242*. Прямая, параллельная стороне АВ = 5 треугольника АВС и проходящая через центр вписанной в него окружности, пересекает стороны ВС и АС в точках М и N соответственно. Найти периметр четырехугольника ABMN, если MN = 3.
243* . В треугольнике АВС на сторонах АВ и АС взяты точки М и IV соответственно так, что AM : МВ = 3:2 и AN : NC = 4 : 5. В каком отношении прямая, проходящая через точку М параллельно ВС, делит отрезок BN?
244* . Через точку пересечения диагоналей трапеции проведена прямая, параллельная основаниям и пересекающая боковые стороны в точках Е и F, причем EF = 8. Найти основания трапеции, если их отношение равно 4.
