Решение задач
12. Случайные величины. Дискретная случайная величина.Закон распределения дискретной случайной величины. Теория вероятностей.
§12. Случайные величины.
Случайной величиной называется переменная X , которая
может принимать различные значения в зависимости от исходов испыта-
ния. Случайные величины могут быть дискретные и непрерывные.
I. Дискретная случайная величина.
Случайная величина X называется дискретной, если она при-
нимает конечное или счетное множество различных значений
{x1,x2,...xn}
с соответствующими вероятностями pi
{p(x1),p(x2),...p(xn)}
.
Закон распределения дискретной случайной величины задается в
виде конечной или бесконечной таблицы;
|
xi |
x1 |
x2 |
... |
xn |
|
pi=p(xi) |
p1 |
p2 |
... |
pn |
в которой значения хi располагаются в строго возрастающем порядке.
Сумма всех соответствующих этим значениям вероятностей равна I,
т.к. все возможные значения случайной величины представляют полную
систему событий,то есть
\begin{equation} \sum\limits_{i=1}^n p_{i}=p_{1}+p_{2}+...+p_{n} =1 \end{equation}
2.Примеры законов распределения дискретной случайной величины.
Пример I. Составить закон распределения числа попаданий в цель
при четырех выстрелах, если вероятность попадания при одном выстре¬
ле равна 0,1.
Решение. Случайная величина X / число попаданий по мишени /
может принимать пять различных значений: 0, I, 2, 3, 4. Соответству-
ющие вероятности находятся по формуле Бернулли:
р4(0) = (0,9)4 = 0,6561 ;
р4(1) =4· 0,1·(0,9)3 = 0,2916 ;
р4(2) =6· 0,12·(0,9)2 = 0,0486 ;
р4(3) =4· 0,13·0,9 = 0,0036 ;
р4(4) =1· 1·(0,1)4 = 0,0001 ;
Закон распределения случайной величины X имеет вид:
|
Число попаданий X |
0 |
I |
2 |
3 |
4 |
|
Вероятность р(*;) |
0,6561 |
0,2916 |
0,0486 |
0,0036 |
0,0001 |
График, соответствующий закону распределения, называется мно¬
гоугольником распределения-случайной величины. Для рассмотренного
примера многоугольник 'распределения представлен на рис.12.1.
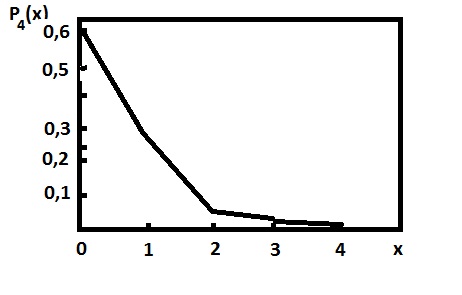
Рис.12.1 '
Пример 2. Биноминальное распределение случайной величины опре¬
деляется формулой Бернулли
Pn (m) = C nm p m q n-m , m=0,1,2,...,n
\begin{equation} \sum\limits_{i=1}^n p_{i}=p_{1}+p_{2}+...+p_{n} =1 \end{equation}
Пример 3. Распределение Пуассона
\begin{equation} P_{n}(m) =\frac{λ^{m}}{m!}e^{-λ} \end{equation}
λ>0 , k=0,1,2,...
\begin{equation} \sum\limits_{i=1}^n p_{i}=p_{1}+p_{2}+...+p_{n} =1 \end{equation}
3.Непрерывная случайная величина.
Случайная величина X называется непрерывной, если она принимает
все значения непрерывно из некоторого множества {X}
В этом случае, соответствующие вероятности значений непрерывной
случайной величины X определяются функцией р(x)которая называется
плотностью распределения вероятностей.
Суммированию по всем значениям вероятностей дискретной случай-
ной величины для непрерывной случайной величины соответствует ин-
тегрированию по всей области {X}
\begin{equation} \sum\limits_{i=1}^n p_{i} =1 \end{equation}
\begin{equation} \int\limits_{-∞}^{∞}p(x)\,dx =1 \end{equation}
Закон распределения непрерывной случайной величины определяется
плотностью распределения вероятностей \(р(x)\) .
стр.25
4;_Примеры законов распределения непрерывной случайной величины.
I. Равномерное распределение /рис.12.2/
\begin{equation} p(x)=\frac{1}{(b-a)}, x∈ [a,b] \end{equation}
\begin{equation} p(x)=0, x∉[a,b] \end{equation}
a и b произвольные числа, b > a.
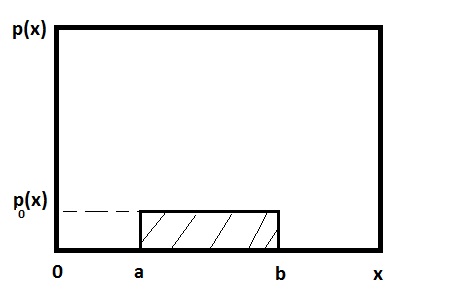
рис.12.2
Площадь заштрихованной области на графике области /рис.12.2/ равна I.
\begin{equation} \int\limits_{-∞}^{∞}p(x)\,dx=\int\limits_{a}^{b}\frac{1}{(b-a)}\,dx=1 \end{equation}
2. Нормальное распределение или закон Гаусса ( рис. 12.3)
\begin{equation} p(x) =\frac{1}{σ(2π)^{ \frac{1}{2}}}e^{-\frac{(x-a)^2}{2σ^2}} \end{equation}
\begin{equation} \int\limits_{-∞}^{∞}p(x)\,dx =1 \end{equation}
σ и a параметры распределения, a - произвольное число,
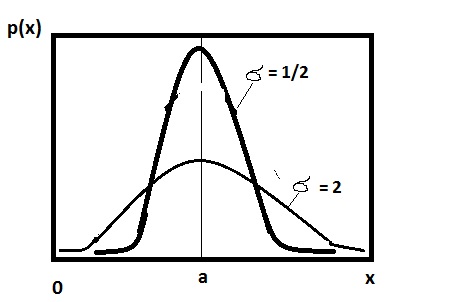
рис.12.3
Закон нормального распределения имеет огромное значение в силу своей универсальности. Uo этому закону распределяются скорости молекул газа /распределение максвелла/,случайные величины при стрельбе, в экономике, социологии и т.д.
Точка х=a характеризует центр распределения или рассеивания вероятностей. Параметр σ характеризует ширину рассеивания случайной величины относительно центра рассеивания.
Показательное распределение
\begin{equation} p(x) =λe^{-λx}, x> 0 \end{equation}
\begin{equation} p(x) =0, x≤0 \end{equation}
Параметр λ>0 .
4. Распределение Коши
\begin{equation} p(x) =\frac{1}{π(1+x^2)} \end{equation}
